5분이면 수포자도 이해되는 삼각함수, 상제관계 역수관계 제곱관계, 삼각함수 가법(덧셈, 뺄셈, 곱셈) 정리 ②

안녕하세요. 여러분의 전기 관련 자격증 취득을 쉽게 할 수 있도록 도와드리는 더불어숲 입니다. 지난 시간에 이어 이번 시간에는 삼각함수의 기본성질인 상호관계, 역수관계, 제곱관계 그리고 삼각함수의 가법(덧셈, 뺄셈, 곱셈)에 대해 말씀드리며 마무리 짓도록 하겠습니다.

 

다음 포스팅을 먼저 읽고 오시면 더욱 이해도가 상승합니다.

5분이면 수포자도 이해되는 삼각함수, 전기(공사)기사 합격보장하는 삼각함수의 기본 개념과 활용방법 ①

 

 

 

삼각함수의 상호관계 _ 상제관계, 역수관계, 제곱관계

 

1. 상제관계 ★ ★ ★

     - sin과 cos을 서로(相, 서로 상) 나누어서(除, 덜(나누다) 제) tan를 만들 수 있다는 점에서 이 등식을 상제관계라고 합니다.

 

$$\tan\theta = \frac{\sin\theta}{\cos\theta} → tan\,\theta cos\,\theta = sin\,\theta$$

$$\cot\theta = \frac{\cos\theta}{\sin\theta}$$

그림 1

 

    위의 그림은 아래와 같습니다.

        ① 사인(sin) θ = $\frac{높이}{빗변} = \frac{B}{C}$

        ② 코사인(cos) θ = $\frac{밑변}{빗변} = \frac{A}{C}$

        ③ 탄젠트(tan) θ = $\frac{높이}{밑변} = \frac{B}{A}$

 

    여기서 sin과 cos의 분모가 C(빗변)로 공통입니다. 정리하면 아래와 같습니다.

    $\frac{\sin\theta}{\cos\theta} = \frac{\frac{B}{C}}{\frac{A}{C}} = \frac{B}{A}$ 이므로

    $\tan\theta = \frac{\sin\theta}{\cos\theta}$된 것입니다. 

 

 

2. 역수관계 

    - 위 그림 1을 보면 사인, 코사인, 코사인은 아래와 같습니다.

        ① 사인(sin) θ = $\frac{높이}{빗변} = \frac{B}{C}$

        ② 코사인(cos) θ = $\frac{밑변}{빗변} = \frac{A}{C}$

        ③ 탄젠트(tan) θ = $\frac{높이}{밑변} = \frac{B}{A}$

 

    - 위에서 사인, 코사인, 탄젠트의 역수는 코시컨트(csc : cosecant) , 시컨트(sec : secant) , 코탄젠트(cot : cotangent)입니다. 이것을 나타낸 것은 아래와 같습니다.

        ① 코시컨트(csc) θ : sin θ의 역수

              $csc\,\theta = \frac{1}{sin\,\theta}$

 

        ② 시컨트(sec) θ : cos θ의 역수

              $sec\,\theta = \frac{1}{cos\,\theta}$

 

       ③ 코탄젠트(cot) θ : tan θ의 역수

             $cot\,\theta = \frac{1}{tna\,\theta}$​

 

    ★ 삼각함수의 역수관계를 쉽게 이해할 수 있는 도식

출처 : 티스토리  Engineering Help

 

 

3. 제곱관계 ★ ★ ★

    삼각함수의 제곱관계는 각 삼각함수의 제곱을 더하면 항상 1이 되는 관계입니다. 여기에서도 피타고라스의 정리가 이용되고 있음을 알 수 있습니다.

     - 예를 들어, 다음과 같은 제곱관계가 성립합니다

        \(\sin^2\,\theta + \cos^2\,\theta = 1\)

        \(\tan^2\,\theta + 1 = \sec^2\,\theta\)

        \(1 + \cot^2\,\theta = \csc^2\,\theta\)

 

    ★ 제곱관계 중 아래 내용은 반드시 암기하시길 바랍니다.

         $\sin^2\,\theta + \cos^2\,\theta = 1$

         $\sin^2\,\theta = 1 - \cos^2\,\theta$

         $sin\,\theta = \sqrt{1 - cos^2\,\theta}$

 

 

4. 예제를 통해 익히기

     예제 1. 역률 $cos\,\theta$ = 0.8일 때, 무효율 $sin\,\theta$를 구하시오

     예제 2. 역률 $cos\,\theta$ = 0.6일 때, 무효율 $sin\,\theta$를 구하시오

     예제 3. 부하가 무유동성 소자일 때 $cos\,\theta$ = 1.0일 때 무효율 $sin\,\theta$를 구하시오

 

    - 풀이

       그림 1을 보면 $cos\,theta$가 역률에 해당합니다. 즉 $cos\,\theta = \frac{A}{C}$ 입니다. 삼각함수의 상호관계 중 제곱관계에서 반드시 암기하고 있어야 한다는 부분 기억하시죠? 이 부분을 가져와 해를 구하면 됩니다.

         $\sin^2\,\theta + \cos^2\,\theta = 1$

         $\sin^2\,\theta = 1 - \cos^2\,\theta$

         $sin\,\theta = \sqrt{1 - cos^2\,\theta}$

 

         $sin\,\theta = \sqrt{1 - 0.8^2}$ = 0.6

 

    나머지 예제 2와 예제 3은 직접 풀어보시길 바랍니다. 여기서 아주 중요한 한 가지를 공개합니다. 사실 이런 문제는 공식과 계산기가 필요 없습니다. 왜냐고요? 여기에도 법칙이 존재합니다. $\sin^2\,\theta + \cos^2\,\theta = 1$이므로 아래와 같은 결과를 볼 수 있습니다. (아래표는 반드시 암기하시길 바랍니다.)

cos θ	sin θ
0.8	0.6
0.6	0.8
1	0
0	1

 

     ★ 참고하면 좋은 내용

삼각함수 - 전력의 관계

        ① 피상전력 $Pa = \frac{P}{cos\,\theta} = \sqrt{P^2 + Pr^2}$

        ② 유효전력 $P = Pa \times cos\,\theta = \sqrt{Pa^2 + Pr^2}$

        ③ 무효전력 $Pr = P \times \frac{sin\,\theta}{cos\,\theta} = P \times tan\,\theta = \sqrt{Pa^2 + P^2}$

        ④ 역률개선 후 유효전력 $P = Pa (cos\,\theta_2 - cos\,\theta_1)$

 

    ▶ 예제 4

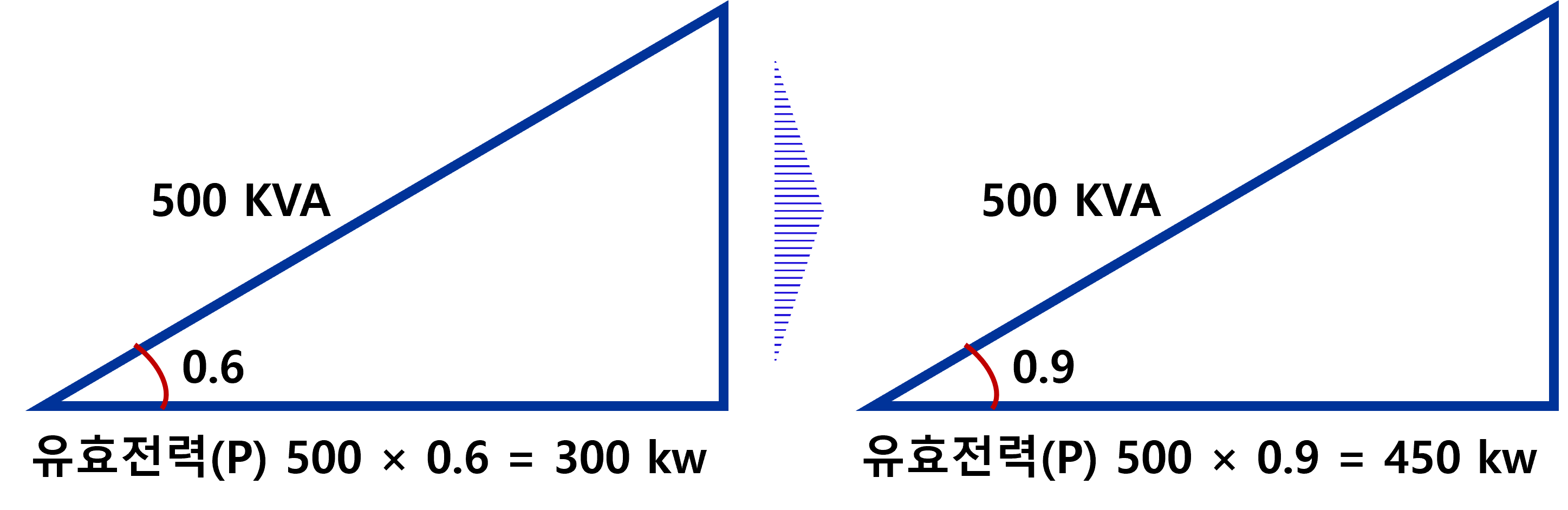
        용량이 500 KVA인 변압기에 역률 60%(지상), 500KVA인 부하가 접속되어 있다. 이 부하와 병렬로 전력용 커패시터를 접속하여 역률을 90%로 개선했을 때, 이 변압기에 증설할 수 있는 부하용량(Kw)을 구하시오 (단, 증설하는 부하의 역률은 90%(지상)이다)

 

    ▶ 풀이

         역률개선 후 유효전력 $P = Pa (cos\,\theta_2 - cos\,\theta_1)$ 500(0.9 - 0.6) = 150 kw

         이 내용이 맞는지 개선 전과 후의 유효전력을 계산해 보면 알 수 있습니다.

삼각함수 - 유효전력

 

 

 

삼각함수의 가법(덧셈, 뺄셈, 곱셈) 정리 ★★★

 

삼각함수의 가법정리란 두 각의 합이나 차에 대한 삼각함수의 값을 구하는 공식입니다. 삼각함수의 가법정리는 다음과 같습니다.

 

    ① $sin(A + B) = sin A \, cos B + cos A \, sin B$ (싸코 뿔 코싸)

    ② $sin(A - B) = sin A \, cos B - cos A \, sin B$ (싸코 마 코싸)

    ③ $cos(A + B) = cos A \, cos B - sin A \, sin B$ (코코 마 싸싸)

    ④ $cos(A - B) = cos A \, cos B + sin A \, sin B$ (코코 뿔 싸싸)

    ⑤ $sin Aㆍcos B = \frac{1}{2}[sin(A + B) + sin(A - B)]$

    ⑥ $cos Aㆍsin B = \frac{1}{2}[sin(A + B) - sin(A - B)]$

 

    ▶ 예제 5

         sin t cos t를 간단히 정리하시오 (이 부분은 제어공학에서 라플라스 변환에 사용됩니다.)

    

    ▶ 풀이

          $sin Aㆍcos B = \frac{1}{2}[sin(A + B) + sin(A - B)]$를 사용하여 간단히 정리하면 아래와 같습니다.

          $sin \,2t = sin(t + t) = 2 \,sin \,t \,cos \,t$ (2를 앞으로 넘기면$\frac{1}{2}$이 되는 것에 주의한다)

          $sin\,t\,cos\,t = \frac{1}{2}\,sin\,2t$

 

    ▶ 예제 6

         $cos \,ωt \,sin\,\theta + cos\,\theta \,sin \,ωt$를 간단히 하시오

 

    ▶ 풀이

          $sin(A + B) = Sin\,A \,cos\,A + cos\,A \,sinB$

          $cos\, ωtㆍsin\,\theta + sin\, ωtㆍcos\,\theta = sin(ωt +\,\theta)$

 

 

지난 시간에 이어 전기 관련 자격증을 취득하기 위해 반드시 정복해야 할 삼각함수에 관하여 알아보았습니다. 삼각함수 내용은 많지만 전기(공사)기사 자격증 취득을 위한 삼각함수는 그렇게 많지 않습니다. 우리는 100점 맞는게 목표가 아니고 합격하는 것이 목표이기 때문에 합격하기 위한 공부를 해야 합니다. 그런 관점에서 포스팅을 한 것이오니 부족한 면이 있다고 판단 되시는 분은 별도로 공부를 더 하시면 되겠습니다. 여러분의 전기(공사)기사 합격을 축하드립니다.