아보가드로의 법칙(Avogadro's law), 기체의 양과 부피 관계 설명

여러분 안녕하세요. 이번 시간에는 위험물 기능장과 위험물 산업기사뿐만 아니라 대다수 자격증 취득을 위해 개념을 반드시 이해하고 있어야 하는 아보가드로의 법칙에 대해 말씀드리겠습니다. 아보가드로의 법칙은 이탈리아의 아메데오 아보가드로가 1812년에 발표한 기체 법칙에 대한 가설입니다. 이 법칙은 모든 기체가 같은 온도, 같은 압력에서 같은 부피 속에 같은 개수의 입자(분자)를 포함한다는 내용입니다.

 

이 법칙에 따르면, 기체의 종류에 관계없이 같은 온도·같은 압력 하에서는 같은 부피 속에 들어 있는 분자의 수가 같으므로 부피가 같은 기체의 무게(또는 밀도)를 비교하면 각 분자의 상대적인 무게를 알 수 있게 됩니다. 예를 들어, 분자량이라는 개념을 사용하면 산소 분자는 32, 질소의 분자는 28, 수소의 분자는 2, 이산화탄소의 분자는 44가 됩니다.

 

아보가드로의 법칙은 온도, 압력, 부피라는 세 가지 변수를 연결시키는 것이 특징입니다. 이 법칙은 가스 법칙과도 밀접한 관련이 있습니다. 이 법칙은 때로는 복잡한 수식으로 표현되기도 하지만, 기본적인 개념을 이해하고 있다면 단순하게 풀어낼 수도 있습니다.

 

같이 보면 좋은 내용 - 밀도(ρ), 비중(S), 비중량(γ)

 

 

 

아보가드로의 법칙(Avogadro's law)

 

아보가드로의 법칙은 이탈리아의 화학자 아메데오 아보가드로가 1811년에 제안한 법칙으로, 기체의 종류가 다를지라도 온도와 압력이 같다면 일정 부피 안에 들어 있는 기체의 입자 수는 같다는 법칙입니다. 즉, 기체의 부피는 기체의 몰수에 비례한다고 할 수 있습니다.

 

이 법칙을 수식으로 표현하면 다음과 같습니다.

 

$$V \propto n$$

 

여기서 $V$는 기체의 부피, $n$은 기체의 몰수입니다. 비례 상수를 $k$라고 하면, 다음과 같이 쓸 수 있습니다.

 

$$V = kn$$

 

이때, $k$는 온도와 압력에만 의존하므로, 온도와 압력이 일정하다면 $k$는 일정한 값이 됩니다. 따라서, 같은 온도와 압력에서는 같은 부피의 기체는 같은 몰수를 가지게 됩니다.

 

아보가드로의 법칙을 이해하기 위해 표나 도표, 그래프를 만들어 보겠습니다. 아래의 그림은 기체의 부피와 몰수의 관계를 나타낸 것입니다.

 

[아보가드로의 법칙을 설명하는 그래프]

 

그래프에서 볼 수 있듯이, 기체의 부피는 기체의 몰수에 비례하여 증가합니다. 즉, 기체의 입자 수가 많아지면 기체의 부피도 커지는 것입니다. 이것이 아보가드로의 법칙의 핵심입니다.

 

아보가드로의 법칙은 화학 반응에서 기체의 양을 측정하거나 예측하는 데 유용하게 사용됩니다. 예를 들어, 수소와 산소가 반응하여 물을 만드는 반응식은 다음과 같습니다.

 

$$2H_2 + O_2 \rightarrow 2H_2O$$

 

이때, 같은 온도와 압력에서 2L의 수소와 1L의 산소가 반응하면, 2L의 물이 생성됩니다. 왜냐하면, 아보가드로의 법칙에 따라서 같은 부피의 기체는 같은 몰수를 가지므로, 2L의 수소는 2몰의 수소, 1L의 산소는 1몰의 산소, 2L의 물은 2몰의 물을 의미하기 때문입니다.

모형으로 나타낸 아보가르도의 법칙, 0℃ 1기압 부피 22.4L

 

 

 

 

아보가드로의 법칙(Avogadro's law) 간단 정리

 

아보가르도의 법칙이란

모든 기체는 같은 온도, 같은 압력에서 같은 부피 속에 같은 개수의 입자를 갖는다는 법칙입니다. 온도와 압력이 같은 조건에서는 기체의 종류가 다르더라도 일정 부피 안에 들어있는 입자 수는 같다는 것입니다.

 

압력(P)과 온도(T)가 같을때, 같은 부피(V)안에 들어있는 기체분자의 수는 기체의 종류에 상관없이 같습니다. 이것을 탄소($C_1$$_2$) 12g에 들어있는 탄소 원자의 수 $6.02×10$^2$$^3$개를 기준으로 1몰(mol) 또는 아보가드로 수로 기준을 잡습니다.

 

​​이때 기체 1몰의 부피는 표준상태(온도 0℃ = 273˚K, 1기압)일때, 기체의 종류에 상관없이 22.4L의 동일한 부피를 가집니다.  ​1몰(mole)의 입자수는 $6.02×10$^2$$^3$ 개(아보가드로수)이고, 이때 표준상태에서 기체 1몰의 부피는 22.4L입니다.

 

즉, 모든 기체 1mole은 표준상태(0℃, 1 기압)에서 부피는 22.4L이고 그 안에는 $6.02×10$^2$$^3$개의 분자가 들어있습니다.  ∴ 기체 1mole = 부피 22.4L = 분자 $6.02×10$^2$$^3$개 (0℃, 1기압)

$1mole \frac{PV}{T} \times \frac{1}{R} (R = \frac{PV}{T} ← 1 mole을 맞추기 위한 상수 임)$

 

$T = 0℃ = 273 + 0℃ = 273˚K, P = 1 기압 = 1 atm$

 

$R = \frac{PV}{1mole \times T} = \frac{1atm \times 22.4L}{1mole \times 273˚K} = 0.082ℓㆍatm/moleㆍ˚K$

 

    1. 기체의 부피는 존재하는 분자의 몰수에 비례한다.

$$V ∝ 몰수 (n) V = 비례 상수(k_4) × n$$

 

    2. 아보가드로의 법칙에 의하면 두 기체가 서로 반응할 때에 그들이 반응하는 부피는 서로 간단한 정수비가 성립한다.

 

    3. 생성물이 기체이면 생성물의 부피와 반응물의 부피 사이에는 간단한 정수비가 성립한다.

기체 반응물과 생성물의 부피 관계

 

 

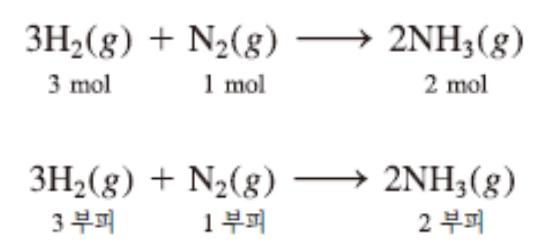
이번 시간에는 여러분과 함께 아보가르도의 법칙에 대해 공부해 보았습니다. 이 법칙에 향 후에 설명할 보일의 법칙, 샤를의 법칙과 함께 하나의 식으로 정리하면 이상기체상태방정식이 유도됩니다. 그러므로 이 내용은 반드시 개념적 이해를 하고 있어야 합니다. 여러분의 위험물 기능장 자격시험 합격을 기원합니다.