위험물 기능장 취득을 위한 기체 법칙 중 이상기체 상태 방정식 완벽 정리

안녕하세요. 여러분의 공부를 도와드리는 더불어숲입니다. 이번 시간에는 기체법칙의 정점에 있는 이상기체 상태 방정식에 대해 공부해 보도록 하겠습니다. 이상기체 상태방정식은 기체의 압력(P), 부피(V), 온도(T) 그리고 몰수(n) 사이의 관계를 나타내는 방정식입니다. 이 방정식은 `PV=nRT`로 표현되며, 여기서 R은 기체상수를 의미합니다.

 

이상기체 상태방정식을 이해하기 위해서는 보일의 법칙과 샤를의 법칙에 대해 알아야 합니다

 

1. 보일의 법칙

일정한 온도에서 일정량의 기체는 압력에 반비례한다. 즉, `PV=k` (k는 일정한 값)입니다.

 

2. 샤를의 법칙

일정한 압력에서 기체의 부피는 온도가 1℃ 오를때마다 0℃때 부피의 $\frac{1}{273}$만큼 증가한다. 즉, 절대온도 (K) = 섭씨온도 (℃) + 273으로 표현할 수 있습니다.

 

이 두 법칙을 결합하면 이상기체 상태방정식이 도출됩니다. 이상기체 상태방정식은 이상기체, 즉 분자간의 상호작용이 무시되고 분자가 차지하는 부피가 무시될 수 있는 기체에 대해 적용됩니다. 이상기체는 대기압과 상온에서 대부분의 기체, 예를 들어 공기 등에 대해 적용될 수 있습니다.

 

기쳅법칙

 

★ 같이 보면 좋을 내용

    1. 보일의 법칙과 샤를의 법칙 그리고 보일ㆍ샤를의 법칙

    2. 아보가드로의 법칙(Avogadro's law), 기체의 양과 부피 관계

 

 

이상기체

 

이상 기체는 그 입자들이 아주 작고, 서로 상호작용하지 않으며, 그들 사이의 거리가 입자 자체의 크기에 비해 아주 크다고 가정합니다.

 

1. 이상기체는 아래의 규칙을 따르는 기체

    - 실제의 기체는 입자끼리 미약하지만 서로 상호작용을 하며, 부피가 매우 작지만 존재하게 됩니다.

     ① 각 기체의 입자는 서로 상호작용이 없다.

     ② 각 기체의 입자는 부피가 없다고 가정한다.

     ③ 기체는 모든 기체법칙을 반드시 따른다.

     ④ 1 atm, 273.15K에서의 기체의 몰부피는 22.4L이다.

  

2. 이상기체와 실제의 기체의 차이

​구분	이상 기체	실제 기체
분자 크기	없음	있음
분자 질량	있음	있음
0˚K에서의 부피	0	0˚K 이전에 액체나 고체로 변함
기체 관련 법칙	모든 법칙을 따른다	고온, 저압에서 거의 일치함
분자 사이의 인력이나 반발력	없음	있음

 

 

3. 이상기체와 실체기체

이상기체의 압력, 부피, 온도와의 관계 그래프

위의 그래프는 기체의 압력(P), 부피(V), 온도(T) 간의 상호작용을 나타내는 그래프입니다. 여기서 주의할 것은 모든 기체가 위의 그래프와 같이 작용하는 것은 아니라는 것입니다. 위의 그래프는 이상기체(ideal gas)를 나타내는 그래프입니다. 이상기체는 실제로 존재하지 않지만, 제각각인 기체들에 대해 위와 같은 기준(표준)을 정한 것입니다.

 

압력(P)에 따른 $\frac{PV}{RT}$의 관계 (좌) 압력이 낮을 수록 이상기체 그래프에 근접한다. (우) 온도가 높을 수록 이상기체 그래프에 근접한다.

 

대부분의 기체들은 위의 그래프처럼 이상기체와 다르게 행동합니다. 다만 수소($H_2$) 와 헬륨($He$)은 이상기체와 근접하여 이상기체에 가깝습니다. 이러한 원소와 분자들은 안정한 결합 또는 상태를 가지고 있고, 헬륨과 같은 18족 비활성기체들은 이상기체에 가깝습니다. 동일한 기체라도 충분히 낮은 압력과 높은 온도에서는 이상기체와 유사해집니다.

 

위의 결과를 토대로 이상기체와 실체기체의 차이를 보면 실제 기체는 압력이 낮을 수록 온도가 높을수록 이상기체에 근접하게 된다는 것을 알 수 있습니다.

 

 

 

 

이상기체 상태 방정식

 

이상기체 상태방정식은 이상기체의 경우에 완벽히 성립하는 압력, 부피, 몰수, 온도에 대한 방정식입니다. 즉, 보일의 법칙, 샤를의 법칙 아보가르도의 법칙을 종합하여 만든 식을 이상기체 상태 방정식이 된 것입니다.

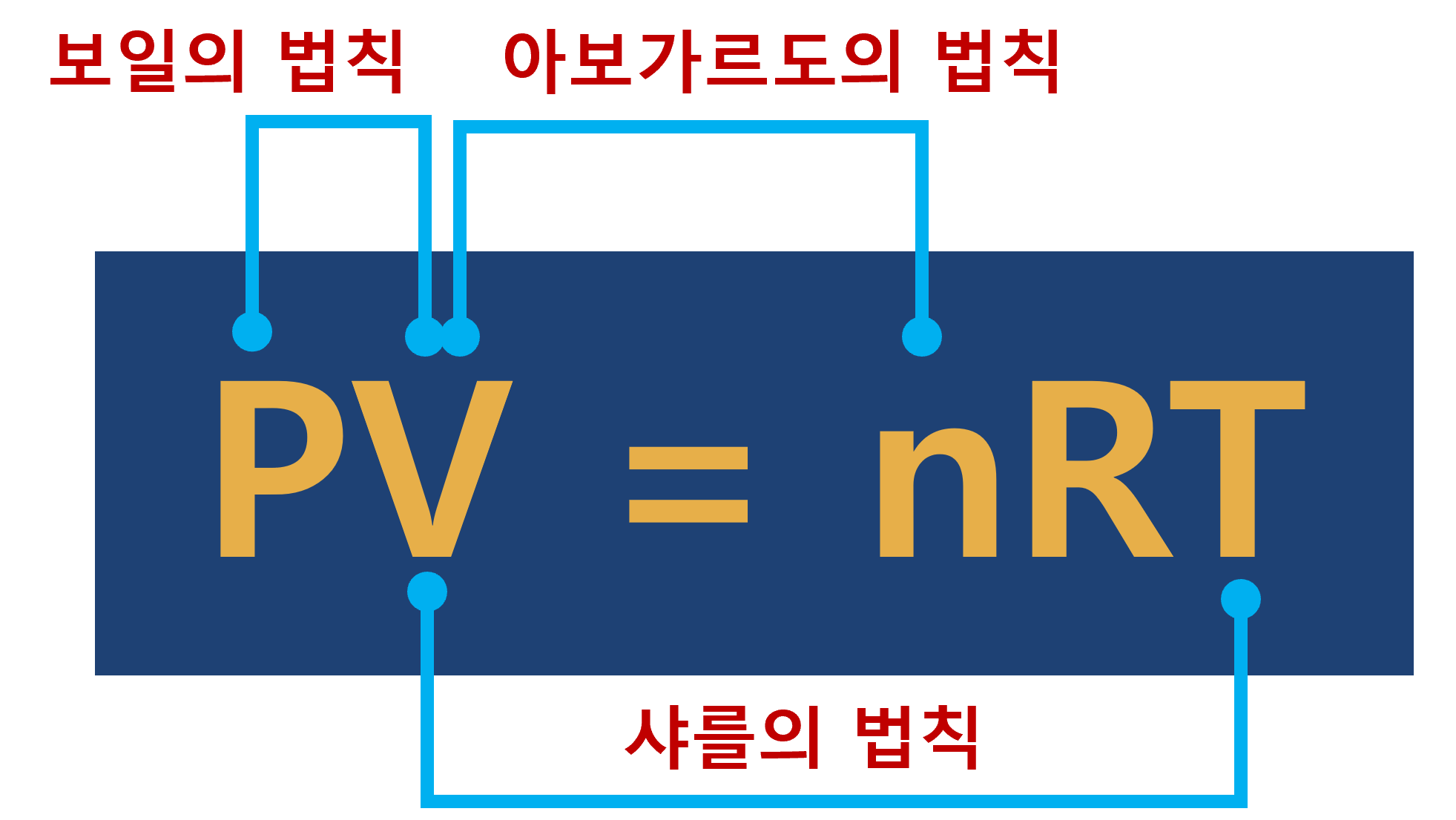
이상기체 상태 방정식은 위와 같이 설명할 수 있습니다. 즉, 부피(V)를 중심으로 압력(P)과의 관계는 『보일의 법칙』, 몰수(n)와의 관계는 『아보가르도의 법칙』,  온도(T)와의 『샤를의 법칙』과의 관계를 가지고 있습니다. 이와 관계된 요소 외에는 모두 일정하다는 것입니다. 

 

 

1. 이상기체 상태 방정식

각각 한가지 변수에 초점이 맞추어진 세 가지 법칙(보일의 법칙, 샤를의 법칙, 아보가르도의 법칙)들은 이상 기체 법칙 혹은 이상 기체 방정식이라는 한 가지 관계식으로 묶을 수 있습니다.

$$PV = nRT \rightarrow n = \frac{PV}{RT}$$

$$PV =\frac{W}{M}RT$$

여기서, P : 압력(atm)

             V : 체적(ℓ)

             n : 몰수(mole) = $\frac{W(질량g)}{M(분자량)}$

            R : 기체상수(아보가르도의 상수)

            T : 절대온도(K : ℃ + 273.15)

 

 

2. 기체 법칙의 응용

이상기체 방정식은 기체의 다른 성질들을 결정 혹은 확인하기 위하여 아래와 같이 고쳐 쓸 수 있습니다.

    $① d(밀도) = \frac{m}{V} = \frac{MP}{RT}$

    $② M(몰질량) = \frac{wRT}{PV} = \frac{dRT}{P}$

     $③ P_t(분압) = P_1 + P_2 + P_3 ......$

            $P_a = Xa × P_t$

 

    ▶연습문제

       1 기압 27℃에서 어떤 기체 3.2g이 2.46ℓ의 부피를 차지하고 있다. 이 기체로 예상되는 물질은 무엇인가? (단, 원자량은 H=1, C=12, N=14, O=16이며 기체상수 R=0.082 atmㆍL/moleㆍ˚K이다)

 

       정답은 여러분이 직접 확인해 보세요. 힌트는 이상기체 상태 방정식($PV =\frac{W}{M}RT$)을 응용한 수식 $M(몰질량) = \frac{wRT}{PV}$을 이용하면 됩니다. 이 응용식에 값을 대입하여 해를 구하면 분자량 32인 산소임을 알 수 있습니다.

 

 

3. 이상기체의 조건

     ① 분자의 크기와 분자 간의 인력을 무시한다

     ② 보일-샤를의 법칙과 이상기체 상태식을 만족한다

     ③ 온도가 높고 압력이 낮을 때 이상기체에 가까워진다

     ④ 실제기체 중 수소(H), 헬륨(He) 가스가 이상기체와 가장 가깝다

 

 

4. 기체상수의 값

기체상수(R) 값	유도 과정
$$0.082ℓㆍatm/moleㆍ˚K$$	$R = \frac{1atm \times 22.4\mathit{l}}{1mole \times 273K} = 0.082\mathit{l}ㆍatm/mloeㆍ˚K$
$$0.082m^3ㆍatm/k-moleㆍ˚K$$	$R = \frac{1atm \times 22.4L \times 1000}{1000 \times 1mole \times 273 ˚K } = 0.082m^3ㆍatm/k-moleㆍ˚K$
$$8.314Paㆍm^3/moleㆍ˚K$$	$R = \frac{101325Pa \times 0.0224m^3}{1mole \times 273 ˚K } = 8.314Paㆍm^3/moleㆍ˚K$ $(1Pa = 1N/m^3, 1J = 1Nㆍm = 1kgㆍm^2/S^2)$
$$1,987cal/moleㆍ˚K$$	$위의 식 × \frac{1cal}{4.184J} (4.184J = 1cal) = 1,987cal/moleㆍ˚K$

 

 

 

5. 이상기체 상태 방정식 적용 시 주의사항

$$PV = nRT \rightarrow n = \frac{PV}{RT}$$

$$PV =\frac{W}{M}RT$$

$$V =\frac{WRT}{PM}$$

 

     ① W의 단위가 [kg] 일 때는 V의 단위는 [$m^3$] 이다

     ② W의 단위가 [g] 일 때는 V의 단위는 [ℓ]이다

     ③ 문제에서 온도 및 압력의 조건이 없으면 표준상태(1 atm, 0℃(273˚K))로 계산한다

          $V =\frac{WRT}{PM}$ → 표준상태는 T=273, R=0.082, P=1 atm 이므로

          $\frac{RT}{P} = \frac{0.083 × 273}{1} = 22.4ℓ$

          $V = \frac{W × 22.4}{M}$을 대입하여 계산해도 무방하다

     ④ 문제의 조건을 잘 보고 단위 틀리지 않게 변환하여 풀어야 한다. (특히 압력과 온도에 주의한다.)

 

 

 

 

마무리

 

1. 기체법칙 요약

보일의 법칙, 샤를의 법칙, 아보가르도의 법칙을 통합하여 하나의 식으로 만들면 이상기체 상태 방정식이 된다.

    ① 보일의 법칙 $V \propto \frac{1}{P}$ (일정한 n과 T)

    ② 샤를의 법칙 $V \propto T$ (일정한 n과 P)

    ③ 아보가르도의 법칙 $V \propto n$ (일정한 P과 T)

 

위 3가지 식을 종합하여 하나의 종합식으로 만든다

$$PV = nRT (4개의 미지수가 존재한다)$$

$$또는$$

$$V = \propto \frac{nT}{P}$$

$$V = R \frac{nT}{P}$$

 

 

2. 이상 기체 방정식(ideal gas equation)

네 변수 P, V, T, n 사이의 관계를 나타내는 식이다. (식이 존재한다는 것은 4개의 미지수 중에 1개는 자동으로 구해진다)

 

 

3. 이상 기체(ideal gas)

압력(P), 부피(V), 온도(T)에 따른 기체의 거동이 이상기체 상태 방정식에 의해 완벽하게 설명될 수 있는 가상의 기체를 말한다.

 

 

4. R(기체상수) 값

    1) 1 atm에서 많은 실제 기체들은 이상 기체처럼 거동 실험 결과 이상 기체 1 mol은 22.4ℓ를 차지한다.

 

    2) 표준 온도와 압력(STP Standard Temperature and Pressure)

          - 0℃, 1 atm의 조건이다. (대다수의 경우 표준상태(STP)는 25℃, 1 atm이다.)이다.)

 

    3) $R = \frac{PV}{nT}$

            $= \frac{1atm \times 22.4\mathit{l}}{1mole \times 273K}$

               $= 0.082 \frac{Lㆍatm}{Kㆍmole}$

               $= 0.082ℓㆍatm/moleㆍ˚K$

 

 

간략히 하려고 했는데 조금 많아졌네요. ^^;;; 그렇더라도 그렇게 어렵지 않은 내용이니 조급해 마시고 천천히 읽어 보세요. 개념이 쉽게 이해될 것입니다. 오늘 배운  이상기체 상태방정식은 기체의 압력(P), 부피(V), 온도(T) 그리고 몰수(n) 사이의 관계를 나타내는 방정식입니다.

 

이상기체 상태방정식은 이상기체, 즉 분자 간의 상호작용이 무시되고 분자가 차지하는 부피가 무시될 수 있는 기체에 대해 적용됩니다. 이상기체는 대기압과 상온에서 대부분의 기체, 예를 들어 공기 등에 대해 적용될 수 있습니다. 지금까지 여러분의 자격시험 합격을 기원하는 더불어숲이었습니다. 감사합니다.