위험물 기능장 취득을 위한 기체 법칙 중 보일의 법칙과 샤를의 법칙 그리고 보일ㆍ샤를의 법칙

안녕하세요. 여러분의 자격시험(위험물 기능장) 합격을 위해 노력하는 더불어숲입니다. 이번 시간에는 기체 법칙의 보일의 법칙, 샤를의 법칙, 보일-샤를의 법칙에 대해 말씀드리겠습니다. 보일의 법칙은 기체의 압력과 부피가 반비례한다는 법칙입니다($P \propto \frac{1}{V}$). 샤를의 법칙은 기체의 부피와 온도가 정비례한다는 법칙입니다($V \propto T$). 보일-샤를의 법칙은 이 두 법칙을 종합한 것으로, 기체의 압력, 부피, 온도 사이의 관계를 나타냅니다. 이상기체 상태방정식($PV = nRT$)은 이 법칙과 아보가드로의 법칙을 종합한 것입니다. 여기서 $P$는 압력, $V$는 부피, $n$는 기체의 몰 수, $R$는 기체 상수, $T$는 절대온도입니다.

 

 

 

같이 보면 좋을 내용 _ 아보가드로의 법칙, 기체의 양과 부피 관계 설명

 

 

 

보일의 법칙

 

보일의 법칙은 기체의 압력과 부피 사이에 반비례 관계가 있다는 법칙입니다. 이 법칙은 온도와 기체의 양이 일정한 닫힌 계 내에서 일정한 질량의 이상 기체가 가하는 절대압력이 그것이 차지하고 있는 부피에 반비례한다는 것을 의미합니다. 보일의 법칙은 다음과 같이 표현될 수 있습니다.

 

$$ P \propto \frac{1}{V} $$

 

여기서 $P$는 기체의 압력, $V$는 기체의 부피를 나타냅니다.

 

    ▶ 일정한 온도에서 일정량의 기체의 부피는 그 기체의 압력에 반비례한다.

$$P_1V_1 = P_2V_2, PV = 일정$$

보일의 법칙

    ▶  연습문제

        압력이 740mmhg에서 320㎖를 차지하는 기체에 온도를 일정하게 하고, 압력을 640mmhg로 하면, 그 부피는 얼마인가?

 

$$P_1V_1 = P_2V_2, P_1 = 740, V_1 = 320, P_2 = 640, V_2 = x라 하면$$

$$740 × 320 = 640 × x ∴ x = 370㎖$$

 

 

샤를의 법칙

 

샤를의 법칙은 기체의 부피와 온도 사이에 정비례 관계가 있다는 법칙입니다. 이 법칙은 압력이 일정할 때 기체의 온도가 높아지면 기체의 부피가 증가하고, 온도가 낮아지면 부피가 감소한다는 것을 의미합니다. 수학적으로 샤를의 법칙은 다음과 같이 표현될 수 있습니다.

 

$$ V \propto T $$

 

여기서 $V$는 기체의 부피, $T$는 기체의 절대온도를 나타냅니다.

샤를의 법칙

 

    ▶ 압력이 일정할 때 일정량의 기체의 부피는 1℃ 상승함에 따라 0℃때의 부피의 $\frac{1}{273}$만큼 증가합니다. 즉, 일정한 압력하에서 기체의 부피는 절대온도에 비례합니다.

$$\frac{V_1ㅍ}{T_1} = \frac{V_2}{T_2}, V_2 = \frac{T_1V_1}{T_1}$$

샤를의 법칙

 

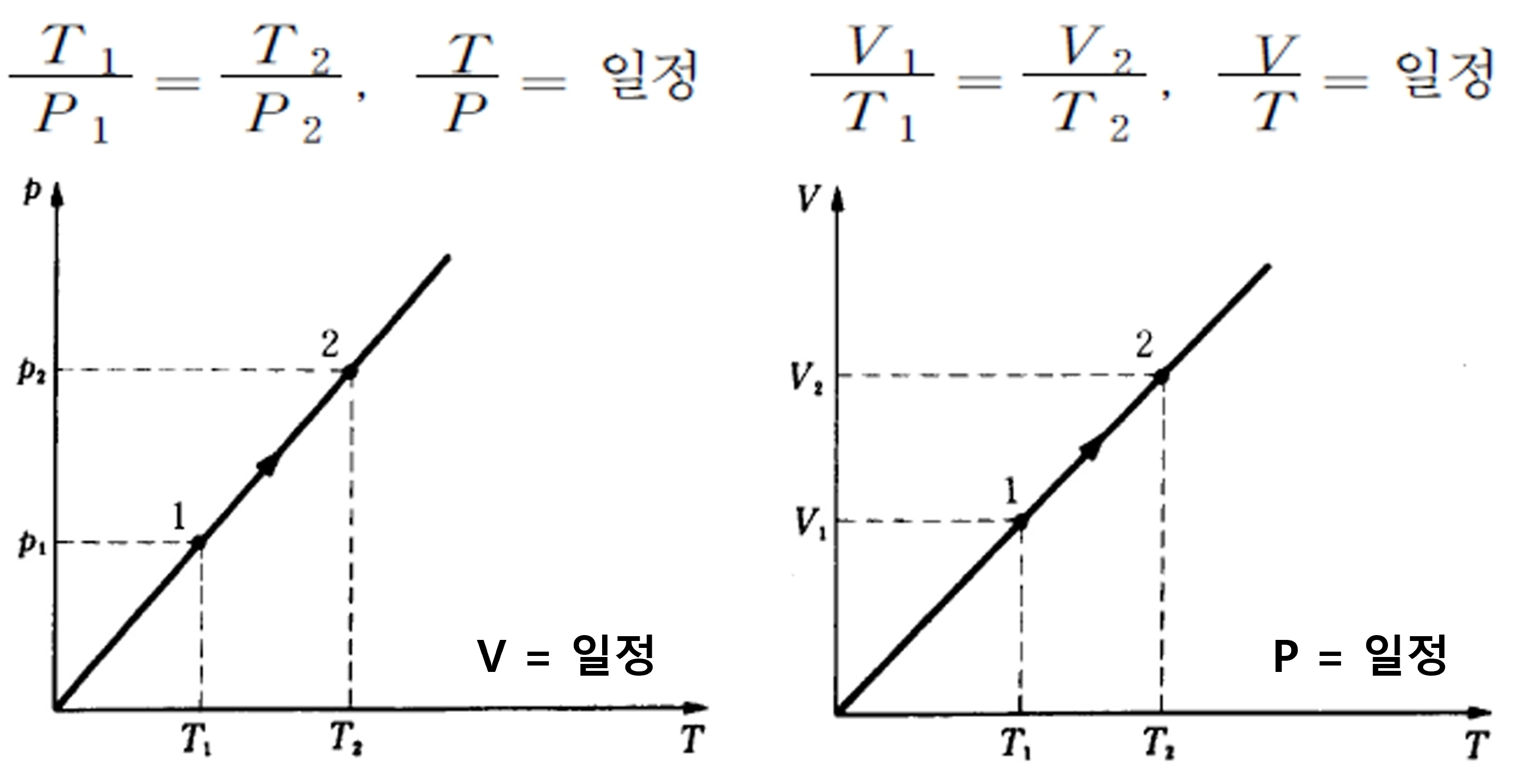
    ▶ 연습문제

         18℃, 760mmhg에서 170㎖의 공기는 0℃ 1 기압에서 그 부피가 몇 ㎖인가?

 

$$\frac{V_1}{T_1} = \frac{V_2}{T_2}, V_1 = 170ml, V_2 = \mathit{X}ml, T_1 = 273 + 18 = 291, T_2 = 273$$

$$\frac{170}{291} = \frac{\mathit{x}}{273} \therefore X = 159.5\mathit{ml}$$

 

 

 

 

보일-샤를의 법칙

 

보일-샤를의 법칙은 기체의 압력, 온도, 부피 사이의 관계를 나타내는 기체 법칙으로, 보일의 법칙과 샤를의 법칙을 종합한 것입니다. 이 법칙과 아보가드로의 법칙을 종합하면 이상기체 상태방정식이 나옵니다. 이상기체 상태방정식은 다음과 같습니다:

 

$$ PV = nRT $$

 

여기서 $P$는 압력, $V$는 부피, $n$는 기체의 몰 수, $R$는 기체 상수, $T$는 절대온도를 나타냅니다.

 

    ▶ 일정량의 기체의 부피가 차지하는 부피는 절대온도에 비례하고 압력에 반비례한다

$$ \frac{P_1V_1}{T_1} = \frac{P_2V_2}{T_2}, P_2 = \frac{P_1V_1T_2}{T_1V_2}$$

보일-샤를의 법칙

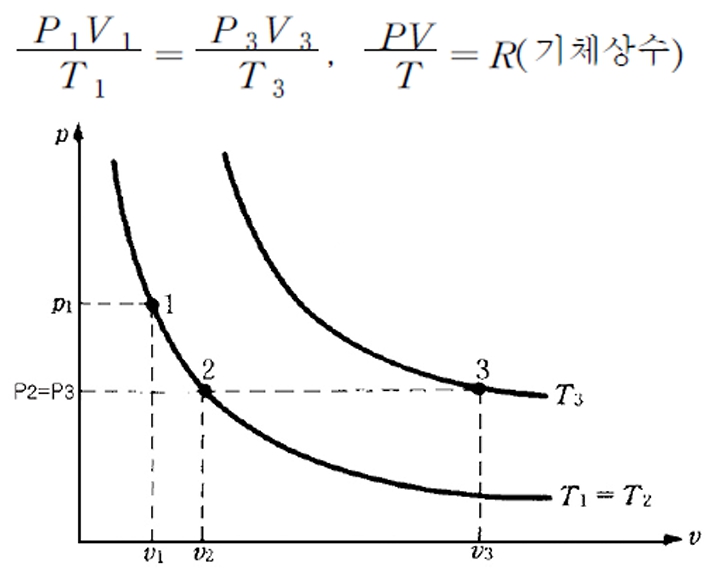
    ▶ 연습문제

         0℃ 1 기압에서 10  ℓ  인 기체가 있다. 273℃ 4 기압에서 기체가 차지하는 부피는 몇 ℓ 인가?

$$ \frac{P_1V_1}{T_1} = \frac{P_2V_2}{T_2}, V_1 = 10\mathit{l}, V_2 = \mathit{x l}, P_1 = 1, P_2 = 4, T_1 = 273, T_2 = 546$$

$$V_2 = \frac{P_1V_1T_2}{T_1p_2}, \frac{1\times 10\times 546}{273\times 4} \therefore 5\mathit{l}$$

 

 

오늘 배운 내용을 다시 한번 정리 후 마무리 하도록 하겠습니다. 보일의 법칙, 샤를의 법칙, 그리고 보일-샤를의 법칙은 기체의 특성을 설명하는 중요한 원리들입니다.

 

1. 보일의 법칙

이 법칙은 기체의 압력과 부피 사이에 반비례 관계가 있다는 것을 나타냅니다. 즉, 온도와 기체의 양이 일정한 닫힌 계 내에서 일정한 질량의 이상 기체가 가하는 절대압력은 그것이 차지하고 있는 부피에 반비례한다는 것입니다.

 

2. 샤를의 법칙

이 법칙은 기체의 부피와 온도 사이에 정비례 관계가 있다는 것을 나타냅니다. 즉, 압력이 일정할 때 기체의 온도가 높아지면 기체의 부피가 증가하고, 온도가 낮아지면 부피가 감소한다는 것입니다.

 

3. 보일-샤를의 법칙

이 법칙은 기체의 압력, 온도, 부피 사이의 관계를 나타내는 기체 법칙으로, 보일의 법칙과 샤를의 법칙을 종합한 것입니다. 이 법칙과 아보가드로의 법칙을 종합하면 이상기체 상태방정식이 나옵니다.

 

이러한 법칙들은 기체의 특성을 이해하고 예측하는 데 매우 중요하며, 열역학, 화학, 물리학 등 다양한 과학 분야에서 활용됩니다. 그러므로 반드시 이해하고 있어야 할 내용입니다. 다음 시간에는 기체 법칙의 완성인 이상기체 상태방정식으로 뵙겠습니다.

 

지금까지 여러분의 합격을 진심으로 원하는 더불어숲이었습니다. 감사합니다.