5분이면 수포자도 이해되는 『부분분수 전개』전기 제어공학 역라플라스 변환 필수 공식

 

안녕하세요. 전기 직종 자격증을 취득하기 위해 노력하는 여러분을 도와드리기 위해 노력하는 더불어숲 입니다. 이번 시간에는 제어공학의 라플라스 변환 문제를 풀어내기 위해서는 반드시 섭렵해야 하는 『부분분수 전개』에 대해 저와 같이 공부하는 시간을 가져보도록 하겠습니다.

 

부분분수 전개는 처음에는 복잡해 보일 수 있지만, 단계별로 살펴보면 이해하기 쉽습니다. 부분 분수 전개의 기본 아이디어는 복잡한 유리식을 더 간단한 분수들의 합으로 나누는 것입니다. 이렇게 하면 각각의 분수를 쉽게 적분할 수 있게 됩니다.

 

 

오늘 배울 부분분수 전개의 공부에 앞서 아래 내용을 먼저 학습하시기를 권해드립니다.

 - 참고 : 5분이면 수포자도 이해되는 전기기초수학 미분

 

 

 

부분분수 전개 - 개요 및 이유

 

"부분분수 전개"는 큰 케이크를 작은 조각들로 나누는 것과 비슷합니다. 큰 케이크가 있으면 한 입 크기로 잘라서 친구들과 나눠 먹기 쉬울 것입니다. 수학에서도 큰 분수를 작은 분수들로 나눠서 각각을 더 쉽게 다룰 수 있습니다.

 

예를 들어, 우리가 큰 케이크를 두 조각으로 나눈다고 한다면, 이 때 수학적으로는 이렇게 쓸 수 있습니다.

 

$$\frac{1}{(x-2)(x-1)}$$

 

이제 이 큰 케이크를 두 조각으로 나눠보겠습니다. 하나는 \(x-2\)만큼의 크기를 가지고, 다른 하나는 \(x-1\)만큼의 크기를 가집니다. 그러면 이렇게 됩니다

 

$$\frac{1}{(x-2)(x-1)} = \frac{A}{x-2} + \frac{B}{x-1}$$

 

여기서 \(A\)와 \(B\)는 케이크 조각의 크기를 나타내는 숫자라고 이해하시면 편안합니다. 우리는 이 숫자들을 찾아야 합니다. 이 숫자들을 찾기 위해서는, 두 조각을 다시 합쳐서 원래의 큰 케이크와 똑같이 만들어야 합니다.

 

이렇게 하면, 원래의 큰 케이크를 두 조각으로 나누고, 다시 합쳐서 원래대로 만드는 과정을 "부분분수 전개"라고 합니다. 이 방법을 사용하면, 큰 분수를 더 쉽게 이해하고 계산할 수 있습니다.

 

 

 

 

 

부분분수 전개 - Cover-up mathod 법

 

부분분수 전개는 기본적으로 항등식의 성질을 이용한다는 것을 기억하고 있으면 됩니다. 항등식은 양변에 같은 값을 곱하거나 대입하거나 해도 등호는 성립한다는 성질을 이용하는 것입니다.

 

- 부분분수 전개를 하는 이유 4가지

    ① 분수식을 간단하게 바꿀 수 있습니다.

    ② 유리식의 적분을 쉽게 할 수 있습니다.

    ③ 유리식으로 나타낸 무한급수의 일반항을 알아낼 수 있습니다.

    ④ 어려운 미분방정식을 역라플라스변환을 통해 쉽게 풀어낼 수 있습니다.

 

Cover-up mathod 법은 유리함수를 여러 유리식으로 분해할 때 계수를 구하는 방법을 말합니다. 이해를 돕기 위해 예시를 통해 말씀드리겠습니다.

 

    ■ One Shot

         부분분수 전개는 유리식의 분모 혹은 분자의 차수를 낮추는 기법으로, 미적분, 라플라스 변환 등 다양한 수학 분야에서 활용됩니다. 

$$\frac{s+3}{(s-8)(s+5)}$$

          위와 같은 유리함수를 분해할 때 계수를 구하는 방법을 Step by Step 방식으로 설명드리겠습니다.

 

         1. 분모를 인수분해 합니다.

             ① 유리식의 분모를 인수분해합니다. 주어진 유리식의 분모 $(s-8)(s+5)$을 아래와 같이 각각의 항으로 나눕니다.

             ② 분모의 각 항을 분수로 설정합니다. 이때, 분자는 임의의 계수(아직 정하지 못한 계수를 말함)로 놓습니다.

$$\frac{s+3}{(s-8)(s+5)} \Rightarrow  \frac{A}{s-8}+\frac{B}{s+5}$$

 

         2. 미지수로 놓은 분자의 계수$(A, B)$를 구합니다.

$$A = \left [ \frac{s+3}{s+5} \right ]_{s=8} = \frac{11}{13}$$

미지수 A값 구하는 방법

             ① 미지수 $A$값을 구하기 위해 $A$의 분모를 지웁니다. 다음으로는 좌측 유리식에서 $A$의 분모와 같은 값을 지웁니다.

             ② 위 그림$ⓑ$과 같이 $A$에 대한 식을 세웁니다.

             ③ $S$값은 ①에서 지운 식$s-8$을 $0$을 만들기 위한 값을 찾으면 됩니다. $0$이 되기 위한 $s$값은 $8$입니다. 그래서 식$ⓑ$에서 $S$값이 8이 된 것입니다.

             ④ $ⓑ$의 식 $s$에 8을 넣어 계산하면 $A$의 값을 구할 수 있습니다.

 

$$B = \left [ \frac{s+3}{s-8} \right ]_{s=-5} = \frac{-2}{-13}$$

미지수 B값 구하는 방법

             - 미지수 $B$의 값 구하는 방법도 위의 미지수 $A$값 구하는 방법과 동일합니다.

 

        3. 1의 식 미지수 A, B에  2에서 구한 각각의 값을 넣어 식을 완성합니다.

$$\frac{s+3}{(s-8)(s+5)} \Rightarrow  \frac{\frac{11}{13}}{s-8}+\frac{\frac{-2}{-13}}{s+5}$$

 

내용이 길어져 집중을 잃지 않기 위해 간단히 정리하면 유리함수의 분모를 오른쪽으로 인수분해 후 미지수 $A, B$를 구해야 합니다. $A$를 구할 때 $A$의 분모를 왼쪽의 유리함수에서 지워버리고 $A$의 분모가 0이 되는 숫자를 대입하면 $A$가 됩니다.

미지수 A값 구하는 방법

 

 

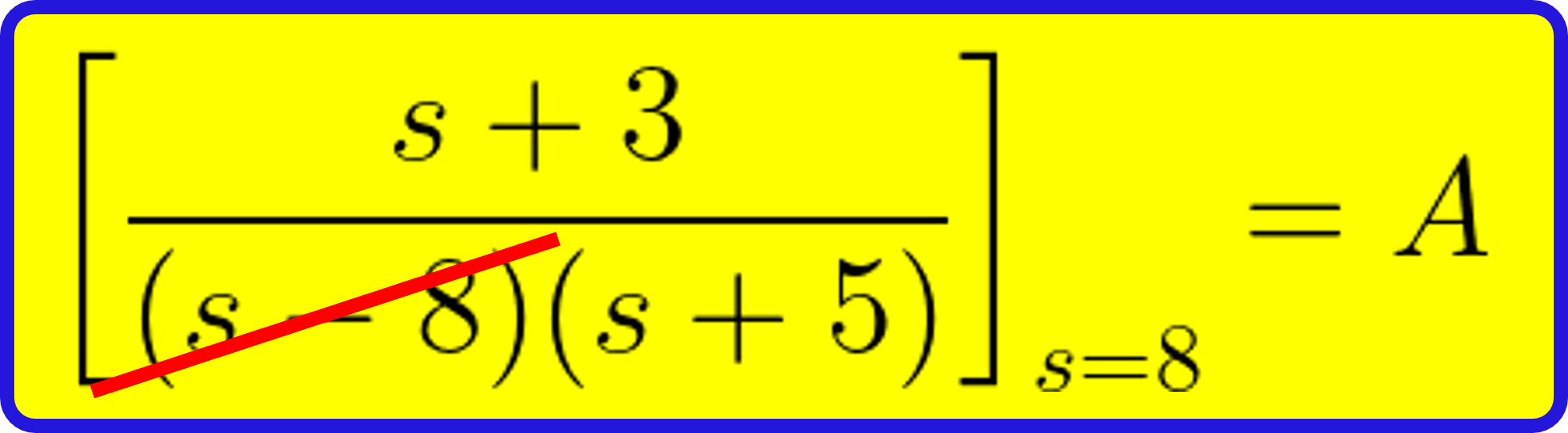
    ■ Two Shot

          - 유리함수가 다음과 같은 경우 부분분수 전개하는 방법입니다.

$$\frac{s+1}{s(s+3)(s-2)}$$

             부분분수 전개는 유리식의 분모 또는 분자의 차수(고차 → 저차)를 낮추는 것을 말합니다. 이런 유리함수도 방법은 위와 같습니다. 즉, 유리함수 분모에서 부분분수 전개를 위해 분모를 각각의 합으로 적고 분자는 임의 숫자(계수)로 놓고 이에 대한 식을 만들면 됩니다.

$$\frac{s+1}{s(s+3)(s-2)} = \frac{A}{s}+\frac{B}{s+3}+\frac{C}{s-2}$$

유리함수에 대한 인수분해식의 미지수 $A, B, C$는 아래와 같이 구해집니다.

$$A = \left [ \frac{s+1}{(s+3)(s-2)} \right ]_{s=0} = \frac{1}{-6}$$

$$B = \left [ \frac{s+1}{s(s-2)} \right ]_{s=-3} = \frac{-2}{15}$$

$$C = \left [ \frac{s+1}{s(s+3)} \right ]_{s=2} = \frac{3}{10}$$

 

지금까지 말씀드린 유리함수의 부분분수 전개 방법을  간단하게 표현하면 아래와 같습니다.

유리함수와 부분분수 전개

 

 

    ■ Three Shot

          - 분모가 아래 유리함수와 같이 제곱 형태인 유리함수의 부분분수 전개 방법입니다.

$$Y(s) = \frac{s}{(s+1)^2}$$

          ① 유리함수에 제곱식이 있는 경우는 고차에서 저차로 차수를 1차까지 낮추어 전개해 주어야 합니다. 즉, 아래와 같이 전개해 주면 됩니다.

$$Y(s) = \frac{s}{(s+1)^2} = \frac{A}{(s-1)^2}+\frac{B}{s+1}$$

          ② 미지수 $A$값을 구합니다. $A$값은 쉽게 구해집니다. $A$의 분모와 유리함수의 분모를 삭제합니다. 남는 것은 $s$만 남게 됩니다. 계산하면 아래와 같습니다.

$$A = \left [ s \right ]_{s=-1} = -1$$

          ③  미지수 $B$의 값을 구합니다.

$$B = \left [ \frac{s}{s+1} \right ]_{s=-1} = \frac{-1}{0} = -\infty$$

                위와 같이 기존 방법대로 풀이하면 결과가 무한대가 되어 오류가 발생하게 됩니다. $B$의 분모 하나와 유리함수의 분모를 삭제하면 1개가 남을 것이라고 생각하면 안 된다는 것을 알 수 있습니다. 이유는 $B$값은 차수가 맞지 않기 때문에 위와 같이 일반적인 방법으로는 구할 수 없습니다. 이런 경우는 『미분』을 통하면 가능합니다.

 

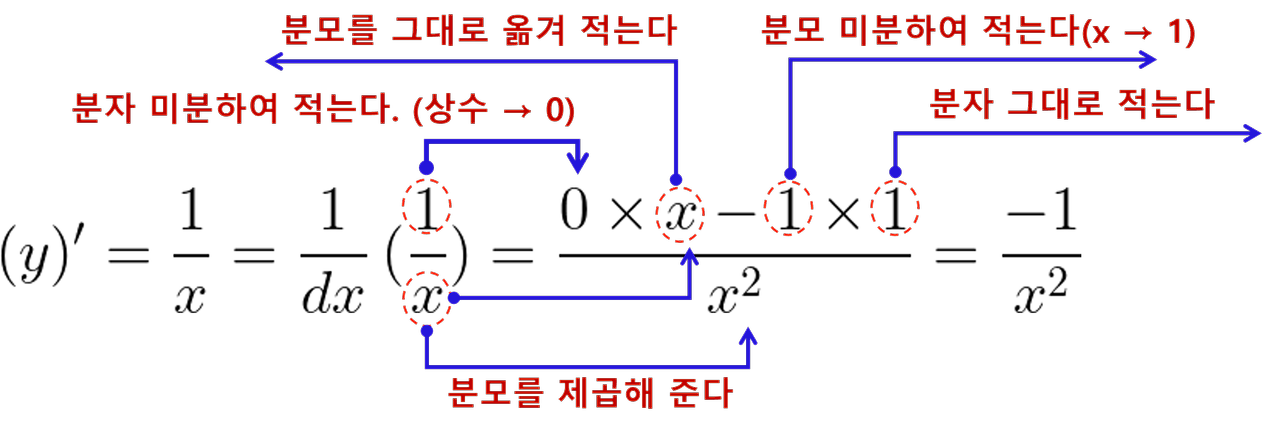
미분하는 이유는 승수를 맞추어주기 위해서입니다. $(s+1)$이 삭제되는 것이 아니고 $(s+1^2$을 모두 삭제할 수 있게 되는 것입니다. 이렇게 하여 남는 것은 $s$만 남게 됩니다. $s$를 미분하면 1이 됩니다.

 

설명이 길었습니다만 간단히 정리하면 "고차를 저차로 즉, 승수를 줄이는 방법으로 해를 구해야 합니다. 승수를 줄이는 방법은 미분을 하면 됩니다. 미분 후 $A$의 분모와 유리함수의 분모를 삭제하면 답을 구할 수 있습니다.

$$B = \frac{\mathrm{d} }{\mathrm{d} s}(s) = 1$$

위와 같이 차수가 부족하므로 미분을 먼저 하는 것입니다.

 

 

    ■ Four Shot

          - 유리함수의 분모가 제곱 형태인 식의 부분분수 전개 방법입니다.

$$Y_{(s)} = \frac{1}{(s+1)^2(s+2)}$$

             머리가 띵 하시지요? ^^ 어려워 마세요. 승수를 낮추어 주는 것에 초점을 맞추면 쉽게 풀 수 있습니다.

             ① 유리함수를 부분분수로 전개하면 아래와 같습니다.

$$Y_{(s)} = \frac{1}{(s+1)^2(s+2)} = \frac{A}{(s+2)^2}+\frac{B}{s+1}+\frac{C}{s+2}$$

             ② 미지수 $A$를 구합니다.

                   - $A$의 분모와 유리함수의 $(s+2)^2$을 삭제하고 정리하면 아래와 같습니다.

$$A = \left [ \frac{1}{s+2} \right ]_{s=-1} = 1$$

             ③ 미지수 $B$를 구하기 위해서는 미분을 해야 합니다. 분수의 미분 방법은 아래 그림을 참조하세요.

분수의 미분 방법

 

                   - $B$는 차수가 맞지 않아 미분을 통해 답을 찾아야 합니다.

$$B = \left [ \frac{\mathrm{d} }{\mathrm{d} s} \left ( \frac{1}{(s+2)} \right ) = \frac{-1\times 1}{(s+2)^2} = \frac{-1}{(s+2)^2}\right ]_{s=-1} = -1$$

 

 

 

문제로 학습하고 이해하기

 

No	문제	부분분수 전개	미지수 계산
1	$$\frac{1}{(s+1)(s+2)}$$	$$\frac{A}{s+1}+\frac{B}{s+2}$$	$$\begin{align}A = \left [ \frac{1}{s+2} \right ]_{s=-1} =1\\B = \left [ \frac{1}{s+1} \right ]_{s=-2} =-1\end{align}$$
2	$$\frac{1}{s(s+1)}$$	$$\frac{A}{s}+\frac{B}{s+1}$$	$$\begin{align}A = \left [ \frac{1}{s+1} \right ]_{s=0} =1\\B = \left [ \frac{1}{s} \right ]_{s=-1} =-1\end{align}$$
3	$$\frac{5s+3}{s(s+1)}$$	$$\frac{A}{s}+\frac{B}{s+1}$$	$$\begin{align}A = \left [ \frac{5s+3}{s+1} \right ]_{s=0} =3\\B = \left [ \frac{5s+3}{s} \right ]_{s=-1} =2\end{align}$$
4	$$\frac{s^2+2}{s(s+1)(s+2)}$$	$$\frac{A}{s}+\frac{B}{s+1}+\frac{C}{s+2}$$	$$\begin{align}A = \left [ \frac{s^2+2}{(s+1)(s+2)} \right ]_{s=0} =1\\B = \left [ \frac{s^2+2}{s(s+2)} \right ]_{s=-1} =\frac{3}{-1}\end{align}$$
5	$$\frac{s+2}{(s+1)^2}$$	$$\frac{A}{(s+1)^2}+\frac{B}{s+1}$$	$$\begin{align}A = \left [ \frac{s+2}{s+1} \right ]_{s=-1} =1\\B = \frac{\mathrm{d} }{\mathrm{d} s} (s+2) = 1\end{align}$$
6	$$\frac{s+2}{(s+1)^2(s+3)}$$	$$\frac{A}{(s+1)^2}+\frac{B}{s+1}+\frac{C}{s+3}$$
	$\begin{align}A = \left [ \frac{s+2}{s+3} \right ]_{s=-1} =\frac{1}{2} \end{align}$ $\begin{align}B = \left [ \frac{\mathrm{d} }{\mathrm{d} s} \left ( \frac{s+2}{s+3} \right ) = \frac{1\times (s+3)-1\times (s+2)}{(s+3)^2} = \frac{s+3-s-2}{(s+2)^2} = \frac{1}{(s+3)^2}\right ]_{s=-1}=\frac{1}{4}\end{align}$
7	$$\frac{1}{x(x+1)}$$	$$\frac{A}{x}+\frac{B}{x+1}$$	$$\begin{align}A = \left [ \frac{1}{x+1} \right ]_{x=0} =1\\B = \left [ \frac{1}{x} \right ]_{x=-1} =-1\end{align}$$
8	$$\frac{1}{(x+1)(x+2)}$$	$$\frac{A}{x+1}+\frac{B}{x+2}$$	$$\begin{align} A = \left [ \frac{1}{x+2} \right ]_{x=-1} =1\\ B = \left [ \frac{1}{x+1} \right ]_{x=-2} =-1 \end{align}$$
9	$$\frac{1}{(x+2)(x+3)}$$	$$\frac{A}{x+2}+\frac{B}{x+3}$$	$$\begin{align} A = \left [ \frac{1}{x+3} \right ]_{x=-2} =1\\ B = \left [ \frac{1}{x+2} \right ]_{x=-3} =-1 \end{align}$$

 

지금까지 제어공학의 라플라스변환을 대비한 부분분수 전개에 대해 말씀드렸습니다. 오늘 공부한 내용을 충분히 연습하시길 바랍니다. 충분히란 문제를 보면 고민하지 않고 바로 풀어낼 수 있을 정도로 연습을 하시기 바랍니다. 오늘 배운 내용 정도면 전기 직종(기사) 자격증 취득에는 문제없을 것으로 보입니다. 여러분의 시험 합격을 기원합니다. 감사합니다.