5분 내 수포자도 이해되는 전기기초수학 적분 - 전자기학, 회로이론에 필수

안녕하세요. 여러분의 전기 관련 시험공부를 편하게 할 수 있도록 도움을 드리는 더불어숲 입니다. 이번 시간에는 전기 관련 시험을 준비하는 분들을 위한 적분에 대하여 말씀드리겠습니다. 적분은 전기 관련  시험에서 중요한 부분이지만, 시험 합격을 위한 공부는 깊이 있게 할 필요는 없습니다. 적분은 전자기학 및 회로이론에서 깊이 있게 관련되어 있고, 간단한 몇 가지 것만 알아두면 충분합니다. 저와 함께 수학이 아닌 전기 관련 적분을 해결하기 위해 세계로 출발해 보시죠!

 

 

적분을 공부하기 전 아래 내용을 먼저 보시기를 추천 드립니다. 많은 도움이 될 것입니다.

1. 5분이면 수포자도 이해하는 행렬과 역행렬, 전기(제어공학, 전력공학) 기초 수학

2. 5분이면 수포자도 이해되는 전기기초수학 미분

 

 

 

 

적분의 개념

 

적분이란 미분의 역과정으로, 어떤 함수의 넓이나 부피를 구하는 방법입니다. 적분은 미분과 반대로 함수의 차수를 높여주는 연산입니다.

 

1. 적분의 기호는 인테그랄이$(\int)$ 입니다. 적분을 할 때는 dx라는 것을 붙여줘야 합니다. dx는 미소한 x의 변화량을 의미합니다.

 

2. 적분을 할 때는 적분 상수를 붙여줘야 합니다. 적분 상수는 임의의 상수로, 적분을 통해 구한 함수에 어떤 수를 더해도 미분하면 원래의 함수가 되기 때문에 붙여주는 것입니다. 적분 상수는 보통 $C$나 $K$로 표시합니다.

 

3. 적분에는 두 가지 종류가 있습니다. 하나는 일반 상수의 적분법이고, 다른 하나는 함수의 적분법입니다. 일반 상수의 적분법은 숫자나 상수에 x를 곱한 함수를 적분하는 방법이고, 함수의 적분법은 x의 거듭제곱이나 다항식과 같은 함수를 적분하는 방법입니다.

 

    1) 일반 상수의 적분법은 다음과 같습니다.

         kx라는 함수를 적분하면 $\int k \, dx = kx + c$ 가 됩니다. 여기서 $k$는 임의의 상수이고, C는 적분 상수입니다. 즉, 상수에 x를 곱한 함수를 적분하면, 상수는 그대로 쓰고, x의 차수를 1 높여주고, 그 수로 나눠주면 됩니다.

상수의 적분 방법

 

    2) 함수의 적분법은 다음과 같습니다.

         $x^n$이라는 함수를 적분하면 $x^(n+1)/(n+1) + C$가 됩니다. 여기서 $n$은 임의의 상수이고, $C$는 적분 상수입니다. 즉, $x$의 거듭제곱 함수를 적분하면, $x$의 차수를 1 높여주고, 그 수로 나눠주면 됩니다.

$$\int x^n \,dx = \frac{1}{x + 1} \, x^{n+1}$$

함수의 적분 방법

    위 내용을 조금 부연 설명하면 이렇습니다. 예를 들어 $x^3$을 적분하면 $x^3$에 차수 1을 더해 $x^4$이 되게 한 후 분모로 내려주면 됩니다. $\frac{1}{4} \, x^4$ 여기서 $x^n$ 값에도 1을 더해주면 식이 완성 됩니다.

 

 

 

반드시 익혀야 할 예제

 

다음 예제는 생각하지 않아도 풀릴 수 있도록 연습하시기를 바랍니다. 전기 직종 시험을 준비한다면 이정도 문제를 풀 수 있는 정도의 지식이면 충분합니다.

 

    ★ 아래 문제 풀이 중 승수는 2 이상을 표기 하는데 굳이 표시한 이유는 여러분의 이해를 돕기 위해서입니다. 

 

1. $y = 3$

    $\int 3 \, dx = 3x$

 

2. $y = 12$

    $\int 12 \, dx = 12x$

 

3. $y = 3x$

    $\int 3x^1 \, dx = \frac{3}{2} \, x^2$

 

4. $y = 12x$

    $\int 12x^1 \, dx = \frac{12}{2} \, x^2 = 6x^2$

 

5. $y = 3x + 1$

    $\int 3x^1 + 1 \, dx = \frac{3}{2} \, x^2 + x$

 

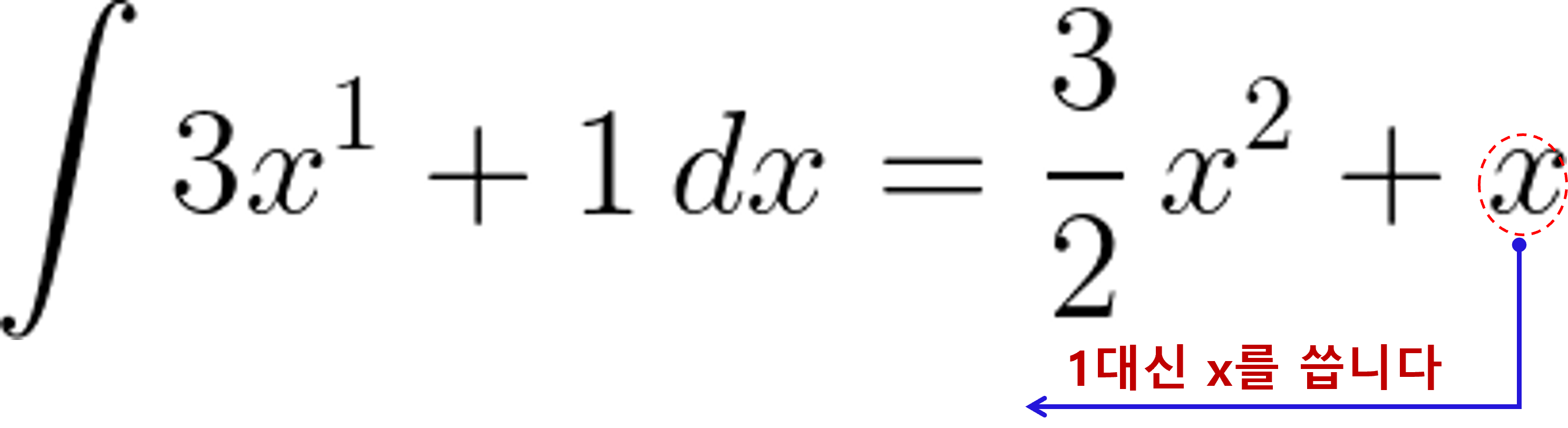
    ▲ 위 5번 형식의 문제는 완벽히 손에 익혀 두세요. 비슷한 문제가 자주 출제되고 있습니다. 전기 직종에서는 이 정도 적분 문제가 가장 어려운 수준이라고 판단이 됩니다.

 

6. $y = 2x + 1$

    $\int (2x^1 + 1) \, dx = \frac{2}{2} \, x^2 + x = x^2 + x

 

7. $y = 4x + 2$

    $\int (4x^1 + 2) \, dx = \frac{4}{2} \, x^2 + 2x = 2x^2 + 2x$

 

8. $y = 2x^2 + x + 4$

    $\int (2x^2 + x + 4) \, dx = \frac{2}{3} \, x^3 + \frac{1}{2}x^2 + 4x$

 

9. $y= 3x^2 + x + 2$

    $\int (3x^2 + x + 2) \, dx = \frac{3}{3} \, x^3 + \frac{1}{2}x^2 + 2x = x^3 + \frac{1}{2}x^2 + 2x$

 

10. $y= 2x^3 + 3x^2 + 4x + 3$

      $\int (2x^3 + 3x^2 + 4x + 3) \, dx = \frac{2}{4} \, x^4 + \frac{3}{3}x^3 + \frac{4}{2}x^2 + 3x = \frac{1}{2}x^4 + x^3 + 2x^2 + 3x $

 

 

 

전기기사 기출문제로 익히기

 

전기기사 기출문제 중 적분과 관련된 문제입니다. 각 문제를 풀어보고, 답을 확인해보세요.

 

1. 다음 중 적분 $\int x^2 dx$의 결과로 옳은 것은?

    (가) $\frac{1}{3}x^3 + C$

    (나) $\frac{1}{2}x^3 + C$

    (다) $x^3 + C$

    (라) $2x^3 + C$

 

    - 정답 : (가) $\frac{1}{3}x^3 + C$

    - 풀이 : x의 거듭제곱 함수를 적분하면, x의 차수를 1 높여주고, 그 수로 나눠주면 됩니다. 따라서 x^2를 적분하면, x^3을 3으로 나눠주고, 적분 상수 C를 더해주면 됩니다.

 

 

2. 다음 중 적분 $\int (2x + 3) dx$의 결과로 옳은 것은?

    (가) $x^2 + 3x + C$

    (나) $2x^2 + 3x + C$

    (다) $x^2 + 6x + C$

    (라) $2x^2 + 6x + C$

 

    - 정답 : (나) $2x^2 + 3x + C$

    - 풀이 : 상수에 x를 곱한 함수를 적분하면, 상수는 그대로 쓰고, x의 차수를 1 높여주고, 그 수로 나눠주면 됩니다. 따라서 2x를 적분하면, 2x^2을 2로 나눠주고, 3을 적분하면, 3x를 더해주고, 적분 상수 C를 더해주면 됩니다.

 

 

3. 다음 중 적분 $\int e^x dx$의 결과로 옳은 것은?

    (가) $e^x + C$

    (나) $e^{x+1} + C$

    (다) $x e^x + C$

    (라) $\frac{1}{x} e^x + C$

 

    - 정답 : (가) $e^x + C$

    - 풀이 : e^x는 자기 자신을 미분하거나 적분하면 자기 자신이 됩니다. 따라서 e^x를 적분하면, e^x에 적분 상수 C를 더해주면 됩니다.

 

 

4. 다음 중 적분 $\int \frac{1}{x} dx$의 결과로 옳은 것은?

    (가) $\frac{1}{x^2} + C$

    (나) $\frac{x}{2} + C$

    (다) $\ln x + C$

    (라) $e^x + C$

 

    - 정답 : (다) $\ln x + C$

    - 해설 : $\frac{1}{x}$는 $\ln x$의 미분입니다. 따라서 $\frac{1}{x}$를 적분하면, $\ln x$에 적분 상수 C를 더해주면 됩니다.

 

 

5. 다음 중 적분 $\int \sin x dx$의 결과로 옳은 것은?

    (가) $\cos x + C$

    (나) $-\cos x + C$

    (다) $\sin x + C$

    (라) $-\sin x + C$

 

    - 정답 : (나) $-\cos x + C$

    - 풀이 : $\sin x$는 $-\cos x$의 미분입니다. 따라서 $\sin x$를 적분하면, $-\cos x$에 적분 상수 C를 더해주면 됩니다.

 

 

이번 시간에는 전기 직종 시험을 준비하는 분들을 위해 전기기초수학 중 적분에 대해 말씀드렸습니다. 늘 말씀드립니다만 자격시험 합격은 60점입니다. 최소 70점 정도 얻을 수 있는 공부법이면 충분하다고 봅니다. 제가 올려드리는 내용은 이러한 관점에서 포스팅을 하고 있습니다. 수험생 여러분의 합격을 기원합니다. 감사합니다.